https://www.nvidia.cn/glossary/k-means/

https://zhuanlan.zhihu.com/p/357072839

聚类与分类的区别

分类：类别是已知的，通过对已知类别的数据进行训练和学习，找到这些不同类的特征，再对未知类别的数据进行分类。属于监督学习。

聚类：事先不知道数据会分为几类，通过聚类分析将数据聚合成几个群体。聚类不需要对数据进行训练和学习。属于无监督学习。

关于监督学习和无监督学习，这里给一个简单的介绍：一般而言，是否有监督，就看输入数据是否有标签，输入数据有标签，则为有监督学习，否则为无监督学习。

K-means 聚类原理简述

聚类算法有很多种，K-Means 是聚类算法中的最常用的一种，算法最大的特点是简单，好理解，运算速度快，但是只能应用于连续型的数据，并且一定要在聚类前需要手工指定要分成几类。

K-Means 聚类算法的大致思想就是“物以类聚，人以群分”：

1. 首先输入 k 的值，即我们指定希望通过聚类得到 k 个分组；
2. 从数据集中随机选取 k 个数据点作为初始大佬（质心）；
3. 对集合中每一个小弟，计算与每一个大佬的距离，离哪个大佬距离近，就跟定哪个大佬；
4. 这时每一个大佬手下都聚集了一票小弟，这时候召开选举大会，每一群选出新的大佬（即通过算法选出新的质心）；
5. 如果新大佬和老大佬之间的距离小于某一个设置的阈值（表示重新计算的质心的位置变化不大，趋于稳定，或者说收敛），可以认为我们进行的聚类已经达到期望的结果，算法终止；
6. 如果新大佬和老大佬距离变化很大，需要迭代3~5步骤。

实例演示

看了上面的原理简述，估计还是有点糊涂，下面举一个非常形象简单的例子。

如下图所示，有6个点，从图上看应该可以分成两堆，前三个点一堆，后三个点另一堆。现在我手工地把 k-means 计算过程演示一下，同时检验是不是和预期一致：

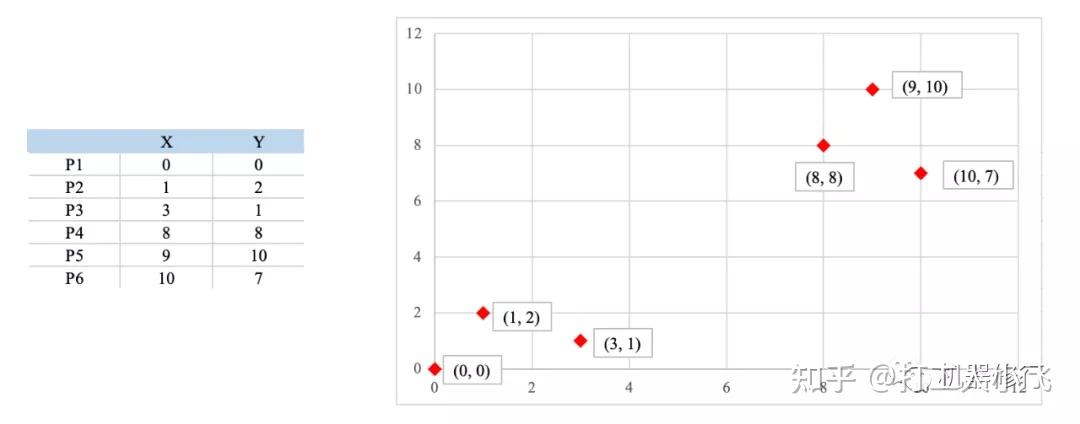
1. 设定 k 值为2；

2. 选择初始大佬（就选 P1 和 P2）；

3. 计算小弟与大佬的距离：

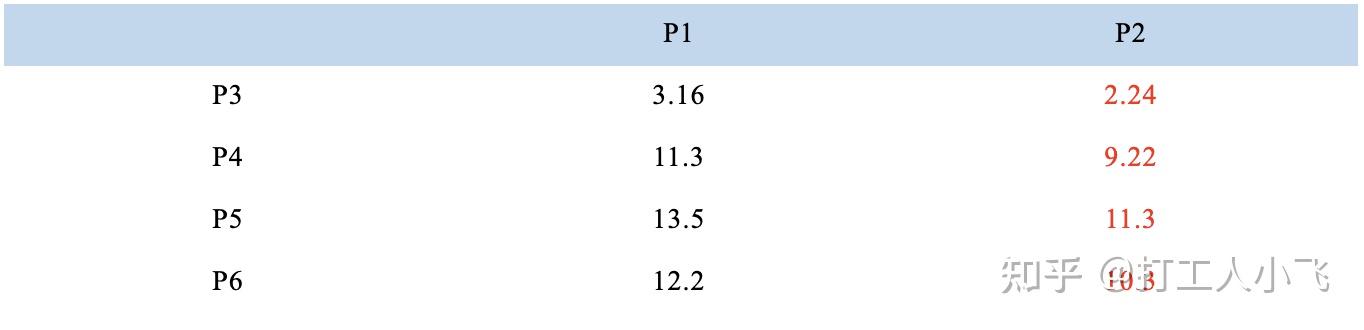
从上图可以看出，所有的小弟都离 P2 更近，所以次站队的结果是：

A 组：P1
B 组：P2、P3、P4、P5、P6

4. 召开选举大会：

A 组没什么可选的，大佬就是自己;
B 组有5个人，需要重新选大佬，这里要注意选大佬的方法是每个人 X 坐标的平均值和 Y 坐标的平均值组成的新的点，为新大佬，也就是说这个大佬是“虚拟的”。

因此，B 组选出新大哥的坐标为：P 哥 ((1+3+8+9+10)/5, (2+1+8+10+7)/5)=(6.2, 5.6)。

综合两组，新大哥为 P1（0，0），P哥（6.2，5.6），而P2-P6重新成为小弟。

5. 再次计算小弟到大佬的距离：

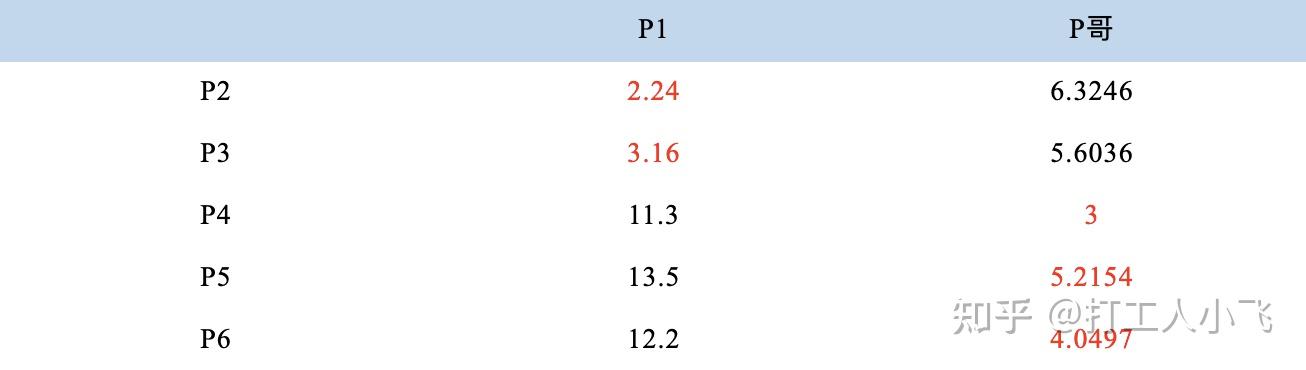
这时可以看到P2、P3离P1更近，P4、P5、P6离P哥更近，所以第二次站队的结果是：

A 组：P1、P2、P3
B 组：P4、P5、P6（虚拟大哥这时候消失）

6. 第二届选举大会：
同样的方法选出新的虚拟大佬：P哥1（1.33，1），P哥2（9，8.33），P1-P6都成为小弟。

7.第三次计算小弟到大佬的距离：

这时可以看到 P1、P2、P3 离 P哥1 更近，P4、P5、P6离 P哥2 更近，所以第二次站队的结果是：
A 组：P1、P2、P3
B 组：P4、P5、P6

我们可以发现，这次站队的结果和上次没有任何变化了，说明已经收敛，聚类结束，聚类结果和我们最开始设想的结果完全一致。

K-means 聚类简易应用示例

关于 K-Means 的算法具体代码，网上有各种版本，这里就不赘述了，下面结合 MATLAB 中的一些函数给出一个较为简洁的版本：

X2 = zscore(X);      % zscore方法标准化数据  
Y2 = pdist(X2);      % 计算距离（默认欧式距离）
Z2 = linkage(Y2);    % 定义变量之间的连接，用指定的算法计算系统聚类树
T = cluster(Z2,6);   % 创建聚类
H = dendrogram(Z2);  % 作出系谱图（散点聚类图看腻了，这里画个系谱图）

当然，MATLAB 以及 sklearn 也提供了相应的 kmeans() 函数可供直接聚类使用，详细参数细节可参考其文档。